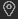消失模鑄造干砂緊實特性的試驗研究
在自制的剪應力測試儀器上,對消失模鑄造干砂緊實特性進行了試驗研究。著重研究了振幅、頻率、振動時間、砂箱大小、形狀以及干砂粒形和粒度等7個因素對干砂緊實特性的影響,并運用正交設計,找到諸因素對緊實特性影響作用大小順序。
關鍵詞:緊實特性;消失模鑄造;影響因素
中圖分類號:TG249.6 文獻標識碼:A
文章編號:1000-8365(2000)02-0042-04
Experimental Study on Compaction Properties of Dry Sand in Expendable Pattern Casting
YANG Mao-sheng,BAO Yin1,
(Inner Mongolia Polytechnic University,Inner Mongolia 010062,China)
LIU Hong-zhi
(Changchun Passenger Train Plant,Changchun 130062,China)
Abstract:In this paper,a experimental study was made on compaction properties of dry sand in the EPC with the
self-made testing device.In detail,the effects of sand box shape,dry sand granularity,amplitude,vibrating time and vibrating frequency on compaction properties of dry sand were
investigated.The relative order of effects was found by experimental design.
Key Words:Compaction properties;Expendable pattern casting; Influencing element;
消失模鑄造因其獨特的工藝性和在成本及環保上的優勢,一經出現就受到鑄造工作者的重視并得到了迅速地發展〔1〕。干砂的振動充填與緊實是消失模鑄造工藝的關鍵技術之一,它不僅要求砂子快速到達模型周圍形成足夠的緊實度,而且在緊實過程中應使模型變形較小,以保證澆注后形成輪廓清晰、尺寸精確的鑄件〔2、3〕。干砂在振動狀態下的充填緊實過程,是1個極其復雜的散粒體動力學過程〔4〕。砂粒在振動過程中必須克服砂粒間的內摩擦力,砂粒―模型以及砂粒―砂箱壁間的外摩擦力以及砂粒本身的重力,才能充滿模型的外型與內腔。可見,干砂緊實特性不僅與砂粒所受的緊實力有關,而且還與砂子本身的特性以及砂箱形狀、大小有關〔5、6〕。基于這1點,本研究通過理論分析并通過實驗測定影響消失模干砂緊實程度的各種因素的作用規律。并利用正交試驗找出各因素對干砂緊實的作用大小以及較好的工藝條件。
1 干砂緊實機理
干砂緊實實質是通過振動臺振動使砂箱內砂粒產生微運動,從而使砂粒體獲得沖量并克服相鄰部位砂粒間的內摩擦阻力而使干砂得到緊實的。在振動臺1個振動周期中砂粒發生不同的運動形態。當振動臺向上運動時,砂粒克服阻力而得到緊實;當振動臺向下運動時,砂粒間的滑移面是該面的剪應力τ與正應力σ的比值達到最大值的平面。當(τ/σ)max>tg?J=f(式中:?J――摩擦角 內摩擦系數),干砂相鄰部位發生移動。本文以微元體作為研究對象。
在干砂中選取,如圖1所示的ABC微元體(dS)。并確定振動周期的1/2作為研究的時間段。設干砂單元體初始動量為Mt,Δt后動量為Mt+Δt。同時認為,1部分干砂經AB邊流入微元體(動量增量為ΔM2,流入速度為U1),另1部分經AC邊流出微元體((動量增量為ΔM1,流出速度為U2)。設干砂微元體只發生移動不發生轉動,即相對剪力數值相等,即如下式:
τxy=τyx
根據質點系動量定理有下式存在
t時刻質點系動量
式中
式中 ρ――干砂緊實度,kg/cm3;
u――為微元體的瞬時速度,m/s;
Δt――為作用時間,s;
τ――干砂剪應力,kpa;
S――微元體的截面積;
θ――滑移面與Y軸的夾角;
LAB、LBC、LAC――為AB、BC、AC邊的長度;
σ――滑移面的正應力,kPa。
由上式可知,影響干砂剪應力的因素有作用時間與干砂緊實速度以及緊實度。而作用時間與振動頻率密切相關;干砂緊實速度決定于振動頻率與振幅以及砂箱固定方式;緊實度與干砂內摩擦系數則與干砂粒度、形狀以及砂箱大小、形狀有關。本研究只研究1/2振動周期的砂粒運動情況,若振動時間t延長,隨之砂粒所獲得緊實沖量的次數增加(t/Δt)。從而使砂粒進一步得到緊實。以上這些影響因素集中體現在干砂剪應力的變化之上,因此本研究以干砂剪應力作為干砂緊實效果的衡量標準,通過測定剪應力,以揭示工藝因素的影響規律。
圖1 微元體
Fig.1 A Tiny Object
2 實驗原理與方法
2.1 實驗原理
據此設計的干砂剪力測試原理,如圖2所示。具體測試方法如下:把干砂均勻地倒入砂箱內,下砂箱固定于振動臺上,在上箱施加剪切力T使干砂Ⅰ―Ⅰ斷面在水平方向移動。發生移動時單位面積的剪力即為干砂的剪應力。
圖2 干砂剪應力測試原理圖
Fig.2 Dragram of test apparatus principle upon shear stress
2.2 實驗裝置
實驗裝置,如圖3所示。它由砂箱、ZS-30J振動試驗臺、壓力傳感器和六筆記錄儀構成。其中振動試驗臺性能參數為:頻率范圍:20~80 Hz;振幅范圍:(0±2) mm。
圖3 實驗裝置圖
Fig.3 The experimental apparatus
2.3 實驗步驟
采用干砂剪切力測試裝置,對不同粒度干砂;砂箱形狀大小;不同振幅和頻率;以及不同振動時間的干砂剪切力進行測定,具體測試時,采用不同法向壓力N,多次測定剪力T的大小。通過線性回歸,求出干砂剪應力τ的關系式:
τ’=σ.tgφ
式中 τ――由于壓重而產生的剪應力,N/m2;
σ――壓重引起的正應力,N/m2;
f――摩擦角。
τ’=τ??總-τf-τ
式中 τf――上下砂箱間摩擦阻力,N/m2;
τ總――所測定的剪應力。
若σ=0 τ=τ??總-τf即儀器測定總的剪應力τ總減去所測定的砂箱間摩擦阻力τf(數值,見表1),即為干砂的剪應力τ。
表1 砂箱間的摩擦阻力系數(砂箱壁厚:8 mm)
Tab.1 Frictional resistance coefficient between boxes
|
小圓砂箱 (φ50×160) mm3 |
大圓砂箱 (φ98×160) mm3 |
方砂箱 (100×105×160) mm3 |
|
|
砂箱面 積/m2 |
1.96×10-3 | 7.54×10-3 | 1.05×10-2 |
|
摩擦阻 力系數 |
0.33 | 0.36 | 0.30 |
3 實驗結果分析
3.1 工藝參數對干砂剪應力的影響
(1)砂箱形狀與大小的影響
采用不同形狀、大小2組砂箱進行各種振動參數下剪應力的測定。結果表明,模數類似而形狀不同的砂箱(模數等于體積與面積之比,體積為干砂體積;面積為砂接觸面積),圓砂箱總是具有較大的剪應力值。對于形狀相同而大小不等的砂箱,大砂箱總是具有較大的剪應力值。
本研究列出在某一振動參數下部分實驗結果,如圖4(a)(b)所示。從圖中可以看出:具有相同模數與高度的圓砂箱比方砂箱干砂緊實效果好,這是因為相比圓砂箱,方砂箱具有較強的邊角摩擦阻力效應,減弱了干砂緊實作用。由于在方砂箱中容易布置模型,所以在實際生產中,方砂箱應用較多;具有相同形狀與高度的大砂箱比小砂箱緊實效果好,這主要因為對于一定量的干砂在其緊實過程中,大砂箱具有較小摩擦阻力作用。
注: 頻率:50 Hz;振幅:0.2 mm;振動時間:60 s;干砂粒度:30目
圖4 砂箱形狀與大小的影響
Fig.4 The effect of shape and size of box
(2)干砂粒度的影響
圖5實驗結果表明,干砂粒度的增大,剪應力增大。原因為干砂粒度越細,其比表面積越大。對于同樣的緊實力,粒度細的緊實阻力(表面間壓力與摩擦力)大,導致剪應力減小。在實際生產中,考慮透氣性與表面粗糙度等工藝因素,一般控制目數在40~70目范圍之內。
(3)振動頻率的影響
一般說來,振動頻率的增大,將導致干砂的摩擦角的下降,提高干砂的流動性,從而增大了干砂的剪應力,根據公式:a=AW2=A(2πf)2,式中 A――振幅;f――頻率;a――加速度。在一定的振幅下,提高振動頻率將加大緊實力,從而提高干砂的剪應力τ,如圖6所示。隨著干砂振動頻率的增加,剪應力增大,當達到50 Hz時,剪應力出現較大值;如果頻率進一步增大,由于受振動臺結構的影響,振幅急劇下降,將導致剪應力的下降。
(4)振幅的影響
注: 頻率:50 Hz; 振幅:0.2 mm;
振動時間:60 s; 砂箱:大圓
圖5 干砂粒度的影響
Fig.5 The effect of sand granules
注: 頻率:50 Hz; 振幅:0.2 mm;
振動時間:60 s; 砂箱:大圓
圖6 振動頻率的作用
Fig.6 The effect of vibrating frequency
振動緊實時,振幅的增大將增加干砂的緊實能量,干砂的剪應力τ隨之提高。受振動臺的結構限制,振幅到一定值時,振動頻率將下降。本實驗采用的頻率為35 Hz,隨著振幅的增大,剪應力變化幅度不大,如圖7所示。在實際生產中,振幅變化范圍較小,一般在1~3 mm之間。
干砂粒度:70目;振動時間:90 s;
注: 頻率:80 Hz;砂箱:大圓;
圖7 振幅的影響
Fig.7 The effect of amplitude
(5)振動時間
由圖8可知,隨著振動時間的延長,剪應力隨之增加。原因為在一定振動工藝參數作用下,振動時間的增加,有利于砂箱與砂粒間以及砂粒之間的相互錯位與移動。從而提高了剪應力τ。但振動時間超過80 s,剪應力τ變化較小。其主要原因是振動臺由振動電機驅動,振動時間過長,將導致激振力方向與其他工藝參數的變化,降低了干砂緊實效果,使τ值下降。在生產操作中〔5〕,若振動頻率為50 Hz,振動加速度為1.2 m/s2,采用40~60 s的振動時間,就可獲得緊實度適當的砂型。
干砂粒度:70目;砂箱:大圓;
注: 頻率:35 Hz;振幅:0.2 mm;
圖8 振動時間的影響
Fig.8 The effect of vibrating time
3.2 工藝因素對干砂剪應力影響作用順序
綜上所述,諸多工藝參數對干砂剪應力有顯著影響,但在實際工藝制定與操作過程中,這些影響因素的主次關系以及同1因素中水平如何選取同樣是至關重要的。利用“正交表”合理安排實驗,可用較少的實驗,經過統計分析得出較優的工藝條件〔8〕。本實驗采用正交設計方法(L18(37×21)),測定并分析各個工藝參數對干砂剪應力的影響程度,實驗結果,如表2所示。首先對所測定數據進行整理,通過方差分析判斷各因子水平的改變對剪應力的影響,M??k,j代表第j列中相應表中水平號為的各實驗數據的總和,其相應的均值為:mk,j=Mk,j/6(k=1,2,3 j=1,2,..,8)。方差
Sj=??3k=16(m??k,j-y)2 式中 y為平均值。
表2 正交實驗結果
Tab.2 Results of orthogonal test
| 試驗號 | 因 素(j=1,2,…,8) |
Yj干砂剪應 力τ N/m2 |
相關系 數γ |
|||||||
|
砂箱結構
(1) |
干砂粒度 (2) |
空 (3) |
振動時間 (4) |
振動頻率 (5) |
振幅 (6) |
空 (7) |
空 (8) |
|||
| 水 平 | ||||||||||
| 1 | 大圓 | 12目 | 1 | 30 s | 35 Hz | 0.1 mm | 1 | 1 | 23476 | 0.925 |
| 2 | 大圓 | 30目 | 2 | 60 s | 42.5 Hz | 0.3 mm | 2 | 1 | 25890 | 0.982 |
| 3 | 大圓 | 70目 | 3 | 90 s | 50 Hz | 0.5 mm | 3 | 1 | 18559 | 0.987 |
| 4 | 方箱 | 12目 | 1 | 60 s | 42.5 Hz | 0.5 mm | 3 | 1 | 19343 | 0.993 |
| 5 | 方箱 | 30目 | 2 | 90 s | 50 Hz | 0.1 mm | 1 | 1 | 17436 | 0.995 |
| 6 | 方箱 | 70目 | 3 | 30 s | 35 Hz | 0.3 mm | 2 | 1 | 6585 | 0.999 |
| 7 | 小圓 | 12目 | 2 | 30 s | 50 Hz | 0.3 mm | 3 | 1 | 16600 | 0.989 |
| 8 | 小圓 | 30目 | 3 | 60 s | 35 Hz | 0.5 mm | 1 | 1 | 4983 | 0.994 |
| 9 | 小圓 | 70目 | 1 | 90 s | 42.5 Hz | 0.1 mm | 2 | 1 | 3192 | 0.998 |
| 10 | 大圓 | 12目 | 3 | 90 s | 42.5 Hz | 0.3 mm | 1 | 2 | 20074 | 0.930 |
| 11 | 大圓 | 30目 | 1 | 30 s | 50 Hz | 0.5 mm | 2 | 2 | 23349 | 0.989 |
| 12 | 大圓 | 70目 | 2 | 60 s | 35 Hz | 0.1 mm | 3 | 2 | 15625 | 0.991 |
| 13 | 方箱 | 12目 | 2 | 90 s | 35 Hz | 0.5 mm | 2 | 2 | 17190 | 0.994 |
| 14 | 方箱 | 30目 | 3 | 30 s | 42.5 Hz | 0.1 mm | 3 | 2 | 20858 | 0.993 |
| 15 | 方箱 | 70目 | 1 | 60 s | 50 Hz | 0.3 mm | 1 | 2 | 16733 | 0.994 |
| 16 | 小圓 | 12目 | 3 | 60 s | 50 Hz | 0.1 mm | 2 | 2 | 22714 | 0.980 |
| 17 | 小圓 | 30目 | 1 | 90 s | 35 Hz | 0.3 mm | 3 | 2 | 3575 | 0.998 |
| 18 | 小圓 | 70目 | 2 | 30 s | 42.5 Hz | 0.5 mm | 1 | 2 | 2708 | 0.999 |
| M1,j | 126973 | 119397 | 89668 | 93576 | 71434 | 103301 | 85410 | 136064 | ||
| M2,j | 98145 | 96091 | 95449 | 105288 | 92065 | 89457 | 98920 | 142826 | T=278890 | * |
| M3,j | 53772 | 63402 | 93773 | 80026 | 115391 | 86132 | 84560 | |||
| m1,j | 21162 | 19900 | 14945 | 15596 | 10906 | 17216 | 14235 | 1548 | Y=15494 | * |
| m2,j | 16358 | 16015 | 15908 | 17548 | 16344 | 14910 | 16487 | 15820 | ||
| m3,j | 8962 | 10567 | 15629 | 13338 | 19232 | 14355 | 15760 | F0.05(2,5) | ||
| fj* | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 1 | =5.79 | |
| Fj | 53.1 | 30.9 | 6.3 | 18.9 | 3.2 | |||||
| Sj | 21289.5 | 16240 | 1717 | 7299 | 12697 | 5257 | 3981 | 1594 | ||
注:f――自由度; Y――剪應力均值; T――剪應力數據之和
表中空列中沒有安排因素,該列僅反映實驗誤差大小,誤差方差為S誤=S3+S7+S8=21336490
表2中數據處理結果表明:S(砂箱結構)>S(干砂粒度)>S(振動頻率)>S(振動時間)>S(振幅)。砂箱結構與干砂粒度對剪應力影響最大;振動頻率與振動時間影響次之;振幅的影響最小。α=0.05顯著性水平計算結果表明:砂箱結構、干砂粒度、振動頻率、振動時間4個因素高度顯著(F1,2,4,5>F0.05(2,5)=5.79),而振幅因素不顯著(F6=3.2<5.79)。所以振幅的影響可忽略不計,考慮到振動臺結構,一般選取低振幅。根據表中數據,選取因素水平所對應最高剪應力的均值,組成較優方案。A(大圓砂箱);B(干砂目數為12目);C(振動頻率為50 Hz);D(振動時間為60 s);E(振幅為0.1 mm)。
4 結論
(1)建立消失模干砂緊實的數學模型,為選定影響因素分析振動工藝參數對剪應力的影響規律提供指導。
(2)通過自制的干砂剪應力的測試儀器進行測定,發現振動工藝參數對干砂緊實程度有顯著的影響;從而使干砂緊實效果定量測試成為可能。
(3)通過對正交試驗結果的數理分析,發現各振動工藝參數對干砂剪切應力的影響大小順序依次為砂箱結構、干砂粒度、振動頻率、振動時間、振幅。
(4)根據本研究實驗條件,工藝參數選取為:砂箱為大圓砂箱;干砂目數為12目;振動頻率為50 Hz;振動時間為60 s;振幅為0.1 mm;可使干砂緊實效果達到較好值。